PART 01Cpk制程能力指数的定义
Cpk制程能力指数,是Complex Process Capabilityindex的缩写,是指在制程管制状态下,制程符合规格的能力。
(1)Cpk的意义
(2)一般以下列的制程特性来衡量制成能力
(3)Ca准确度的定义
准确度Ca (Capability of Accuracy ) : 实际中心与规格中心的差异称为准确度,在制程上,实际中心与规划中心的差异越小,准确度就越高,制程越理想。
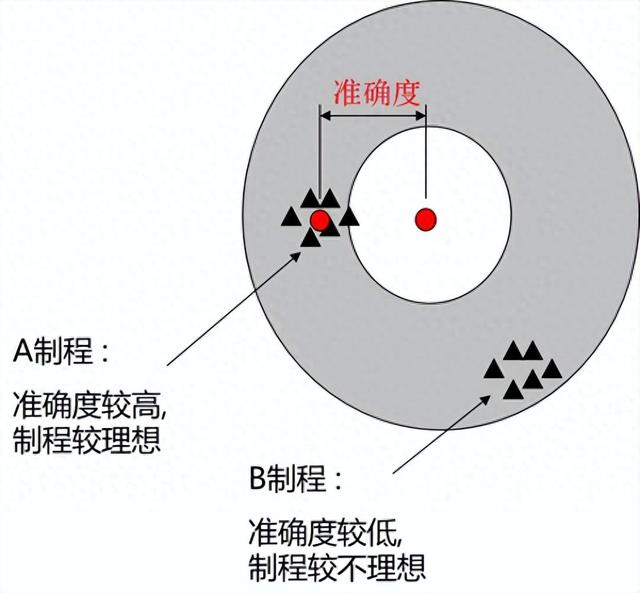
(4)Cp精确度的定义
精确度Cp (Capability of Precision ) ,品质特性的散布范围大小或集中程度称为精确度,在制程上,散步范围(或称变异)越小,精确度越好,制程越理想。
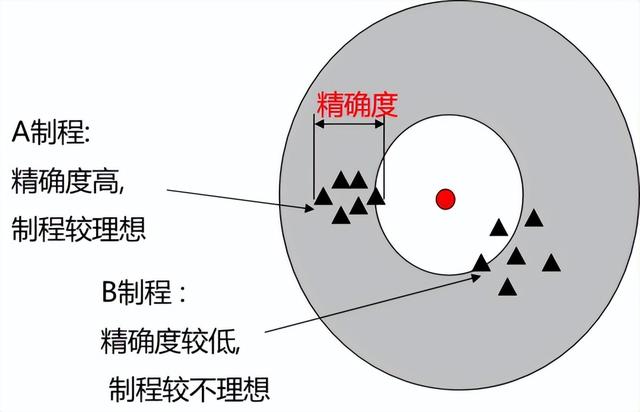
(5)Ca, Cp, Cpk 的相互关系
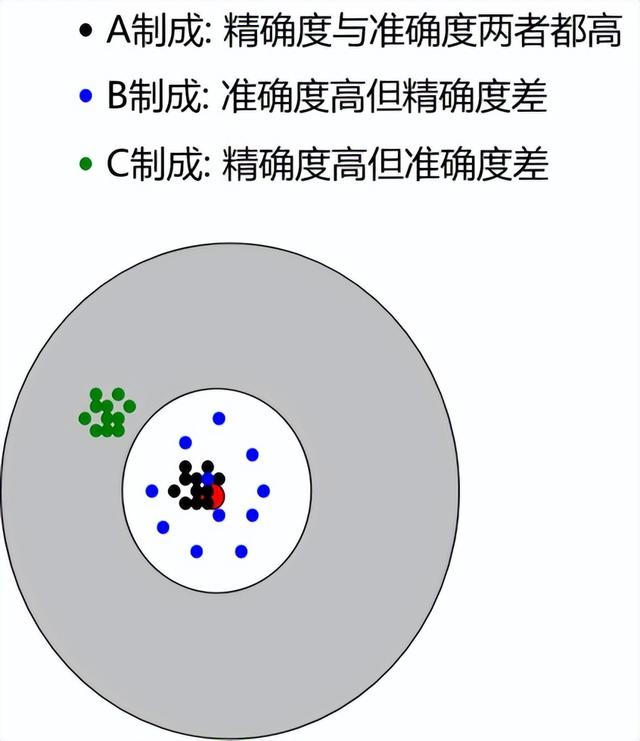
制程能力的要求 :
合格==>准确度要高
稳定==>精确度要好
由以上的要求可知,所有制成中,A是最理想
PART02Ca, Cp, Cpk 的计算
(1) 相关参数的定义
介绍Cpk,Ca, Cp计算方式之前,先介绍一下以下几个概念:
(2) 准确度Ca的计算
01 准确度Ca的计算公式 :
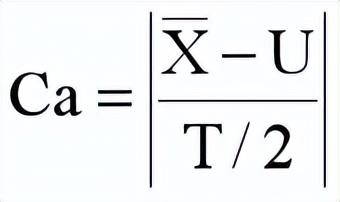
说明 :
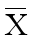
:平均数
U:规格中心值
T:规格上限 – 规格下限
02 准确度Ca的等级定义

03 准确度Ca的计算范例
设计产品规格为3.5mm±0.1mm, 今在量产线上抽测5个样品, 其测量值如下:3.52, 3.53, 3.57, 3.54, 3.53,则Ca值计算如下:
U=3.50, T=3.6-3.4=0.2,
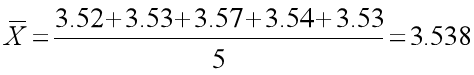
,
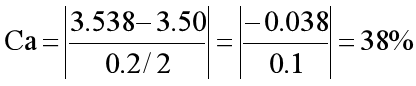
,
为等级C,务必进行持续改善制成。
(3)精确度Cp的计算
01 精确度Cp的计算公式
双边规格:
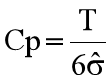
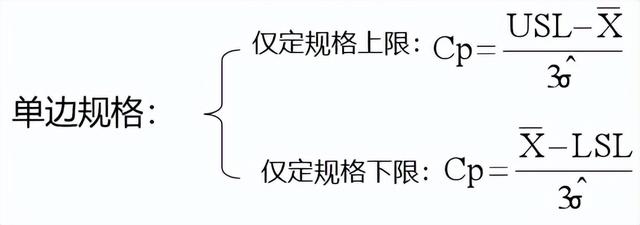
;单边规格:

说明:
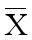
: 平均数
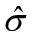
: 标准差
T : 规格上限 – 规格下限
USL : 规格上限
LSL : 规格下限
注意事项:
由公式可知,Cp是不考虑制程的中心点
标准差计算最好采用以下标准差的定义公式:(通常用于计算单组数据)
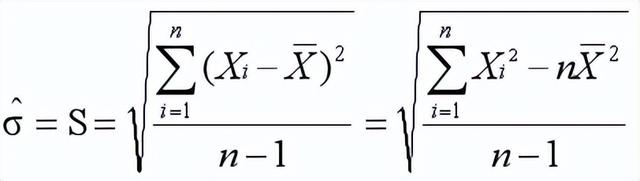
若无适当的计算机运算,则标准差也可用下面的建议公式计算,该方法一般适用于多组数据的情况下:
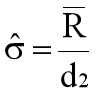
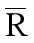
: 极差的平均值(每组数值的极差总和的平均值)
极差=一组数据中的最大值-最小值
d2 : 请查阅附录d2系数表(d2取值附录表)
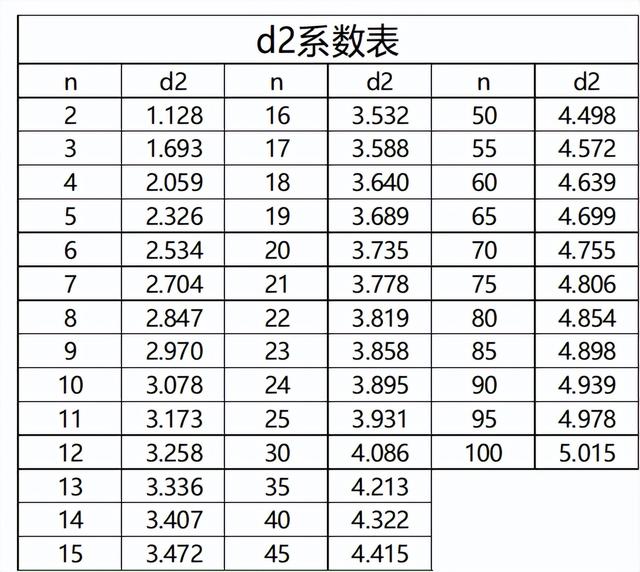
02 精确度Cp的等级定义
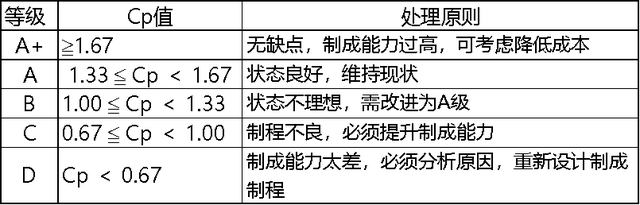
03 精确度Cp的计算范例
T=3.6-3.4=0.2,
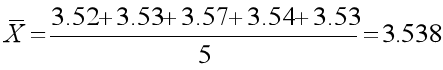
σ=

=0.0192,
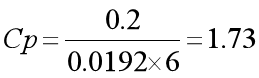
大于1.67,等级为A+,制成能力优秀,可降低制成,降低成本

(4)制成能力Cpk的计算
01 制成能力Cpk的计算公式
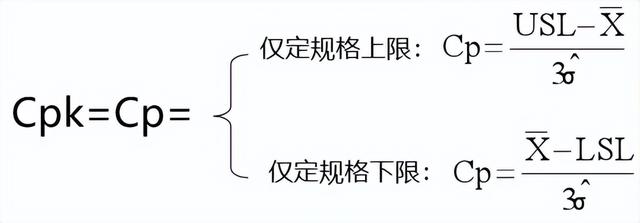
02 制成能力Cpk的等级定义
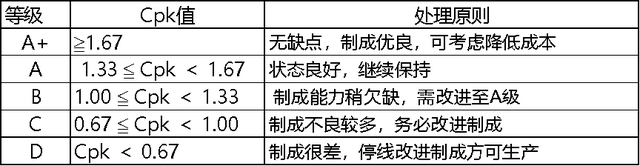
03 制成能力Cpk的计算范例
Cpk 练习范例(双边规格):设产品设计规格值为:3.5mm±0.1mm, 今在稳定量产线抽检5个样品,测量数据如下:3.52, 3.53, 3.57, 3.54, 3.53, 则Cpk计算如下:
σ=0.0192(前面过程已经介绍其计算过程,这里就不做累述)
USL=3.6, LCL=3.4,
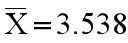
采用如下公式计算:
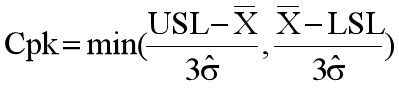
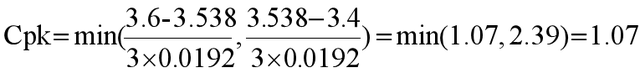
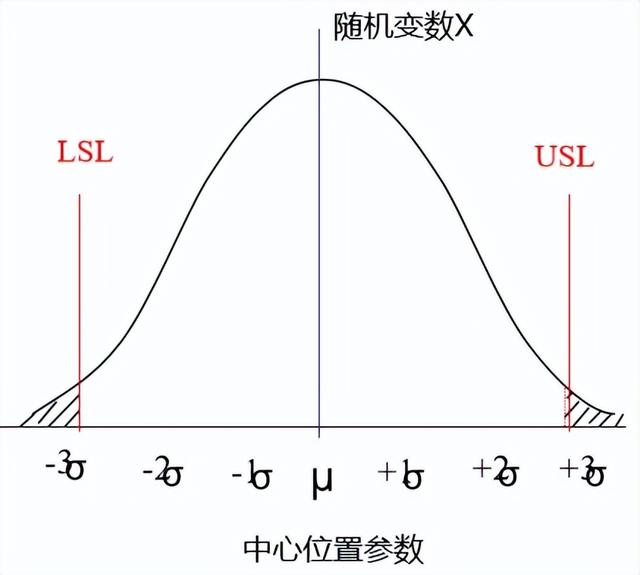
PART03制成能力与不良率的对照关系
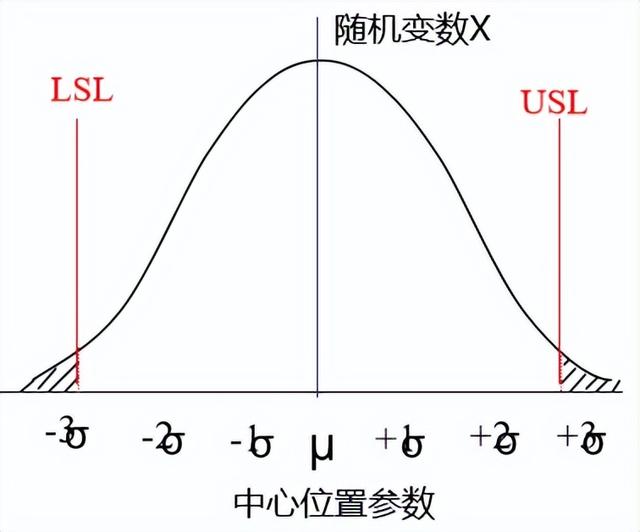
(1)Ca, Cp 与不良率的关系
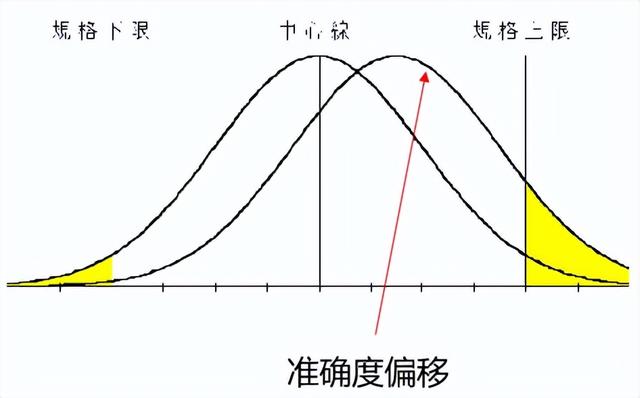
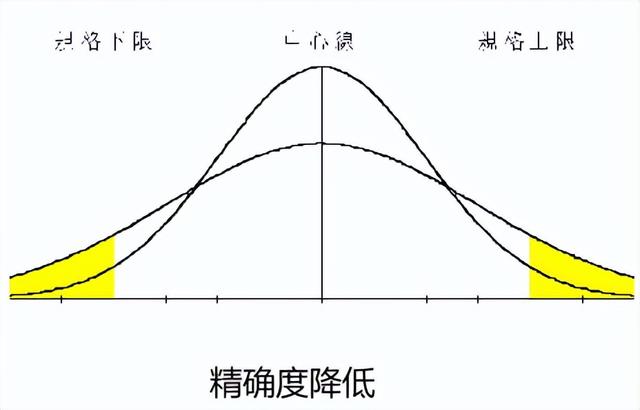
黄色阴影区域表示为超出6σ之外的不良率
(2)Cpk 与不良率的关系
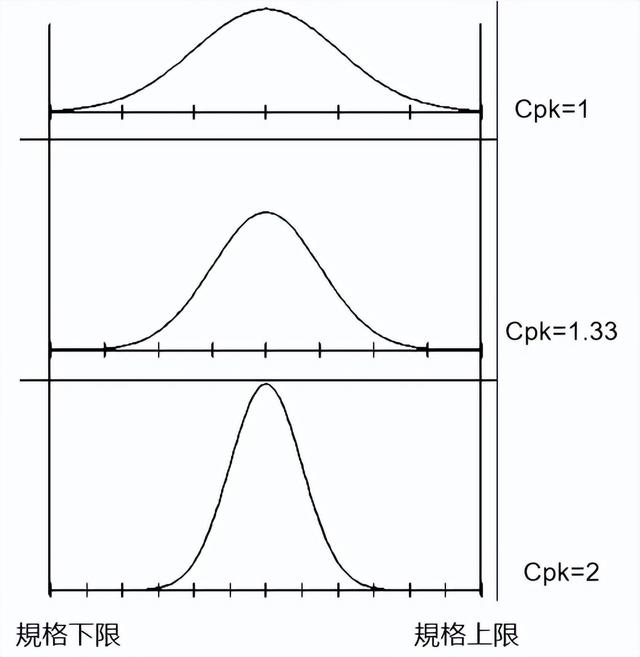
(3)Cpk 数值与不良率的对照表
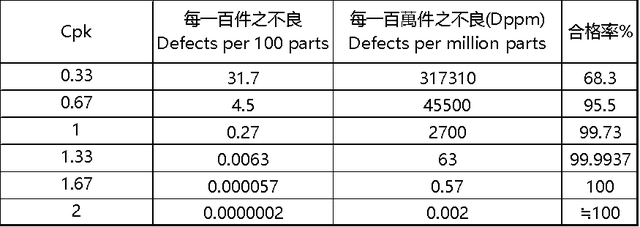
数据分布在正态情况下,换算才有意义!
PART04Ca, Cp, Cpk的计算总结表
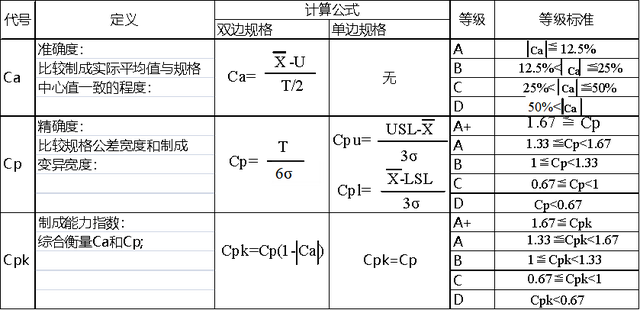
PART05Cpk 计算的数据采集
Cpk 的计算依据是来自于收集的收据,所以数据的收集及正确是计算Cpk的根本,通常数据收集有以下观点:
组内一般为3--5个取样,习惯上取3或者5没有见过4个,以体现R极差;
我们希望组内体现出特殊原因;
组间一般为天数或小时,可以为20或者整个月,我们希望组间体现分布中的一般
50为统计学内大样本的数量
100 数量越多越具有代表性
PART06Cpk 计算标准模板
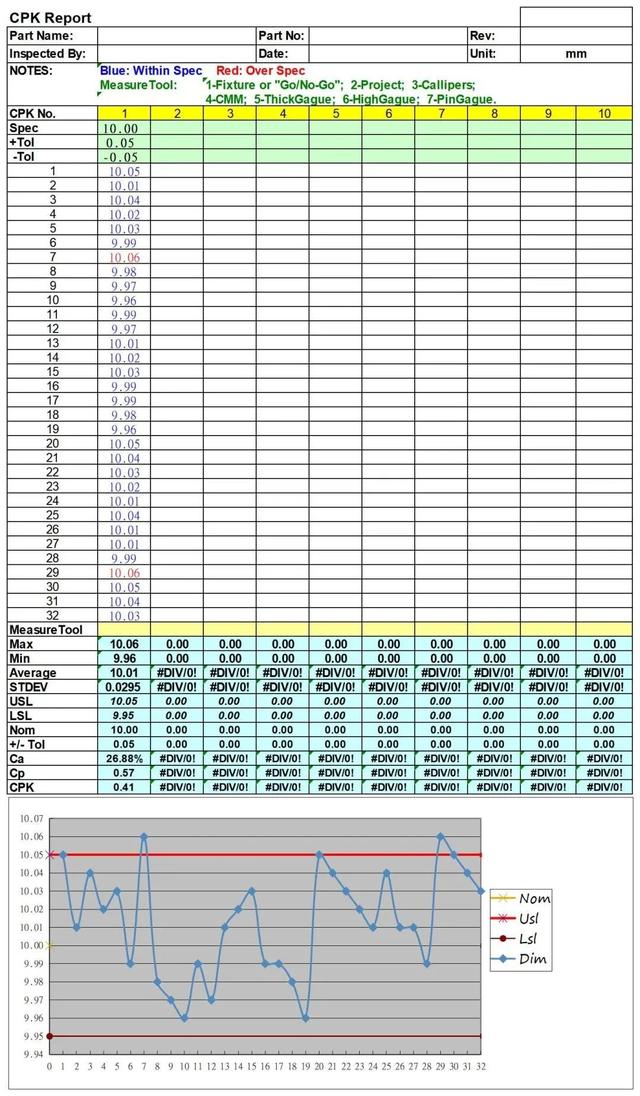
评论列表 (0条)